
Matematik hayatımızın her yerinde ve dünya algımızın şekillendiren en değerli etmen. Matematikçi Ian Stewart, 2013 yılında bir kitap yazdı ve tarihin akışını değiştiren 17 matematiksel denklemi ele aldı. İşte o denklemler ve bilime katkıları;
Kaynak: http://www.businessinsider.com/17-equati…
1. Pisagor Teoremi
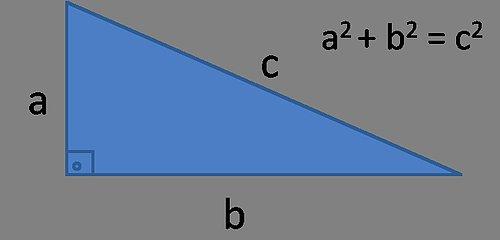
Bu denklem insanlığın uzambilgisinin temellerini atmıştır. Pisagor teoremine göre bir dik üçgende dik kenarın yani hipotenüsün bir kenarını oluşturduğu karenin alanı öteki iki dik kenarın birer kenar olarak oluşturdukları karelerin alanları toplamına eşittir. Bu bağ, eğimli Öklitçi olmayan geometriyi olağan ve düz olan Öklitçi geometriden ayrıştırmaktadır. Örneğin, bir kürenin yüzeyine çizilecek üçgen bu denklemden faydalanamaz.
Teorem sonradan İÖ 6. YY’da Yunan filozof ve matematikçi Pisagor’a ile isimlendirildi ancak Hindu, Yunan, Çinli ve Babilli matematikçiler teoremin ögelerini, Pisagor yaşamadan çok evvel bilmekteydiler. Pisagor teoreminin bilinen birinci ispatı Öklid’in Elementler yapıtında bulunabilir.
2. Logaritmalar
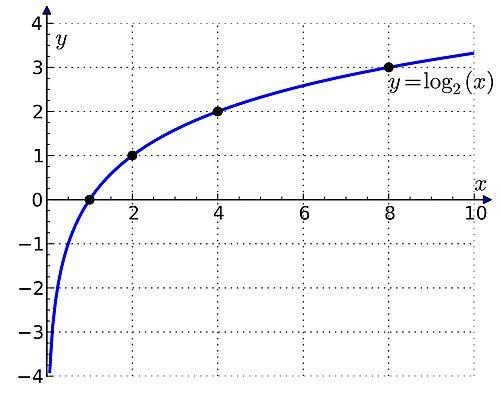
Logaritma, üstel fonksiyonların karşıtı olan bir matematiksel işlevdir. Örneğin 1000’in 10 tabanına nazaran logaritması 3’tür zira 1000, 10’un 3. kuvvetidir; 1000 = 10 × 10 × 10 = 10 üssü 3. Logaritma, üstel fonksiyonların zıddının hesaplanmasına duyulan muhtaçlık sonucu ortaya çıkmıştır. Örneğin 2’nin kübü 8’dir. Burada 3’ü tabir etmek için logaritmaya muhtaçlık vardır.
Logaritma 17. yüzyılın başında John Napier tarafından hesaplamaları kolaylaştırmak için oluşturuldu. Denizciler, bilim insanları, mühendisler ve daha süratli hesap yapmak isteyen şahıslar tarafından benimsenen logaritma, hesap cetvelleri ve logaritma tabloları aracılığıyla kullanılabiliyordu. Uzun vakit alan çok basamaklı çarpma süreçleri logaritmalar sayesinde kolaylıkla yapılabiliyordu. Dijital teknolojinin gelişmesine kadar, çok haneli sayılarla süreç yapmak için kullanılabilecek en uygun yol logaritmalardı.
3. Kalkülüs
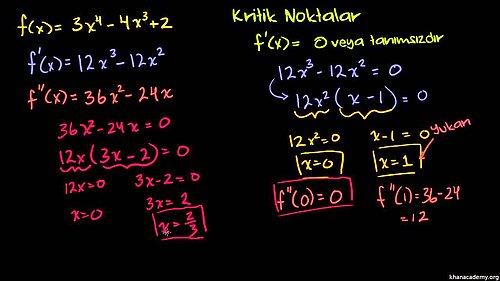
Kalkülüs cebir, trigonometri ve analitik geometri konularının üzerine inşa edilmiştir. Kalkülüs matematiğin bir alt kısmı olan matematiksel analizin giriş kısmıdır ve işlev, limit, türev, integral, diziler, seriler vb. bahisleri içerir.
Kalkülüsün geçmişi genelde antik çağ, orta çağ ve çağdaş çağ olmak üzere farklı evrelere ayrılır. Newton ve Leibniz modern manada türev denklemini birbirlerinden bağımsızca yazmışlardır ve Kalkülüs tarihinin en kıymetli isimlerindendirler.
Kalkülüs hareket ve değişken içeren her türlü modelde, yani hayatın istisnasız her alanında kullanılır. Örneğin tabiat bilimleri, bilgisayar bilimleri, istatistik, mühendislik, iktisat, iş ömrü ve tıp başta olmak üzere matematiksel modellemenin gerektiği ve en uygun tahlil testlerinin istendiği alanlarda kullanılmaktadır.
4. Kütle çekimi

Isaac Newton gök cisimlerinin hareketleriyle ilgili yaptığı çalışmalar sonucu kütlelerin birbirine uyguladığı çekim kuvvetini keşfetmiştir. Bu yüzden; bu kanuna Newton’ın kozmik kütle çekimi yasası adı verilmiştir.
Kütle çekimi, objelerin birbirlerine gerçek çekme kuvveti uygulamasına denir. Newton’ın kozmik kütle çekimi yasasının sistemi; bir nokta kütle (m1) öbür bir nokta kütleyi (m2) iki kütlenin çarpımı ile yanlışsız, ortalarındaki (r) uzaklığının karesi ile aksi orantılı olacak büyüklükteki bir F2 kuvveti ile çeker. Kütlelerden ve bu kütlelerin ortalarındaki uzaklıktan bağımsız olarak |F1| ve |F2| kuvvetlerinin büyüklükleri her vakit birbirine eşittir ve G kütle çekimi sabitidir.
5. Karmaşık Sayılar
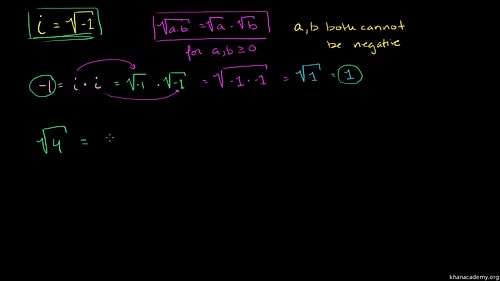
Doğal sayılardan negatif sayılara, kesirli sayılardan gerçek sayılara, matematikçiler hangi sayıların gerçekten olduğu fikrini daima ileri taşımaktalar. -1’in kare kökü i ile söz edilen -1’in kare kökü karmaşık sayıları ortaya çıkararak gerçek sayı kavramını bir üst boyuta taşımaktadır.
Matematikte karmaşık sayı, bir gerçel bir de sanal kısımdan oluşan bir objedir. Matematikte bu sayıların uzayı olarak C gösterilir. Bu harfin seçilmesinin nedeni İngilizce’de karmaşık sözcüğünün karşılığının complex olmasıdır. Bütün gerçel sayılar sanal kısımları sıfıra eşit olan birer karmaşık sayı olarak düşünülebilir. Başka bir deyişle gerçel sayılar, karmaşık sayı düzleminde gerçel sayılar ekseni üzerinde bulunurlar. Karmaşık sayı, iki boyutlu kartezyen koordinat sisteminde, nokta yahut pozisyon vektörü olarak gösterilebilir. Sayılar alışılageldiği üzere yatay bileşen gerçel kısmı ve düşey (dikey) bileşende sanal kısmı olarak çizilir.
6. Euler Formülü
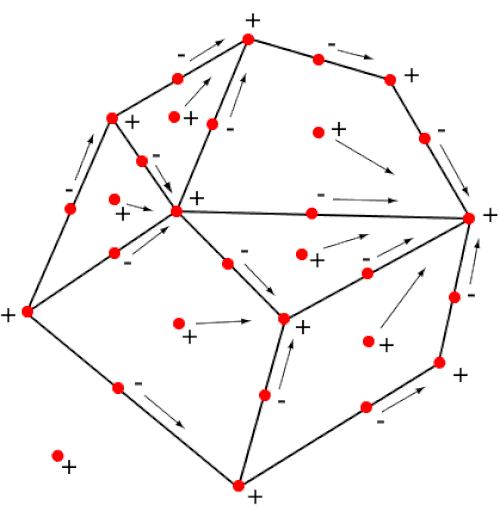
Her bir çokyüzlü için K (köşe sayısı) + Y (yüz sayısı) − A (ayrıt-kenar sayısı) sayısını hesaplarsak her vakit sonucun 2 olduğunu görürüz. Euler’in bu formülü tüm konveks (dışbükey) çokyüzlüler için geçerlidir.
Euler formülü’nde x yerine değişkenler konularak yeni bağıntılar türetilebilir. Bu bağıntılardan yaralanılarak yeni trigonometrik bağıntılara varılabilir ve tekrar bir kümenin alt küme sayılarını veren Bell Sayıları’nı veren üreteç işlevine da kompleks değişkenler verilerek trigonometrik analog bulunabilir.
7. Olağan Dağılım
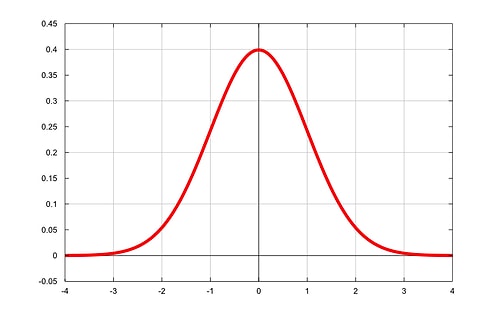
Olağan dağılım, tıpkı zamanda Gauss dağılımı veya Gauss tipi dağılım olarak isimlendirilen, birçok alanda pratik uygulaması olan, çok değerli bir sürekli mümkünlük dağılım ailesidir.
Bir olasılık dağılımını çeşitli halde matematiksel tabirlerle karakterize etmek mümkündür. Bunlar ortasında göze en güzel hitap edeni olasılık yoğunluk fonksiyonu ile olur. Dağılımın özellikleri ayrıyeten birikimli dağılım işlevi, momentler, kümülantlar, karakteristik işlev, moment üreten işlev, kümülant üreten işlev ve Maxwell’in teoremi vasıtasıyla da belirtilebilir.
8. Dalga Denklemi
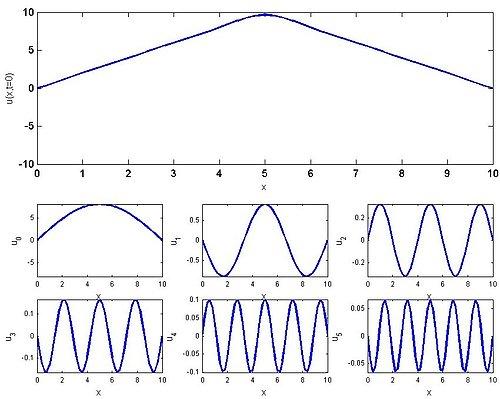
Dalga denklemi fizikte çok değerli yere sahip bir kısmi diferansiyel denklemdir. Bu denklemin tahlillerinden ses, ışık ve su dalgalarının hareketlerini betimleyen fizikî nicelikler çıkar. Kullanım alanı akustik, akışkanlar mekaniği ve elektromanyetikte epeyce fazladır. Elektromanyetik dalga denklemi, elektromanyetik dalgaların ortam boyunca ya da bir vakum ortamı içerisinde yayılmasını açıklar. Akustik dalga denklemi ise, akustik dalgaların bir ortamda yayılımını düzenler.
9. Fourier Dönüşümü

Fourier Dönüşümü, insan konuşması üzere çok daha karmaşık olan dalga yapılarının anlaşılması için temel bir denklemdir. İşlevleri diğer işlevlere çeviren dönüşüm sistemidir. Temeli her integrallenebilir işlevin çeşitli genlikte ve frekansta sinüs ve kosinüs fonksiyonlarının toplamı biçiminde yazılabilmesine dayanır.
Fourier açılımı sayesinde işlevlerin frekansı çarçabuk belirlenebilir. Bu yaklaşım farklı dönemlerde girdiye maruz kalan sistemlerin çıktısını ve çıktısının frekansını belirlemekte kolaylık sağlar. Fourier Dönüşümü, günümüzde modern sinyal sürece, tahlil ve veri sıkıştırmanın temelini oluşturmaktadır.
10. Navier-Stokes Denklemleri

Navier-Stokes Denklemleri sıvılar ve gazlar üzere akışkanların hareketini tanımlamaya yarayan bir dizi denklemden oluşmaktadır. Bu denklemler akışkan içerisindeki ünite kütleye tesir eden momentum değişimlerinin, basınç değişimleri ve sürtünme kayıplarına neden olan viskoz kuvvetlerin toplamına eşit olduğunun doğruluğunu ortaya koymaktadır. Bu viskoz kuvvetler moleküller ortası etkileşimlerden meydana gelmekte ve akışkanın akmaya ne kadar dirençli olduğunu göstermektedir. Böylelikle, Navier-Stokes denklemlerinin, verilen akışkanın rastgele bir bölgesindeki kuvvetler dengesinin dinamik ifadesi olduğu söylenebilir.
Gerek akademik gerekse ekonomik birçok fenomenin fiziği Navier-Stokes Denklemleri ile açıklamaktadır. Hava akımları ve okyanus akıntılarının, boru içindeki su akışının, galaksideki yıldız hareketlerinin, kanat etrafındaki hava akımlarının modellenmesinde ve hesaplarında sıkça kullanılırlar.
11. Maxwell Denklemleri

Maxwell denklemleri Lorentz kuvveti yasası ile birlikte klasik elektrodinamik, klasik optik ve elektrik devrelerine kaynak oluşturan bir dizi kısmi türevli (diferansiyel) denklemlerden oluşur. Bu alanlar çağdaş elektrik ve haberleşme teknolojilerinin temelini oluşturmaktadır. Maxwell denklemleri elektrik ve manyetik alanların birbirilerini, yükler ve akımlar tarafından nasıl değiştirildiği ve üretildiğini açıklamaktadır. Bu denklemler, İskoç fizikçi ve matematikçi olan ve bu denklemlerin birinci biçimini yayınlayan James Clerk Maxwell’ in ismi ile isimlendirilmiştir.
Maxwell eşitliğinin katılığı içerdiği büyüklüklerin ne kadar kesin tanımlandığına bağlıdır. Kurallar ünite sistemine nazaran değişir, zira ışık suratı üzere boyutsuz çarpanlar tarafından emilerek çeşitli tarifleri ve boyutları değişebilmektedir.
12. Termodinamiğin İkinci Yasası
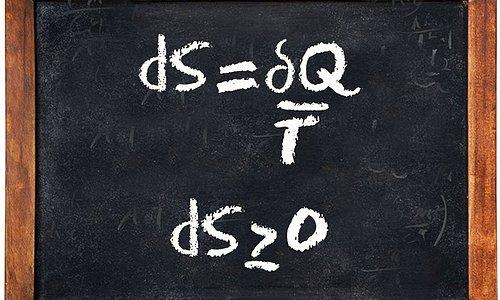
Termodinamiğin ikinci yasası veya ısıldevinimin ikinci yasası, izole sistemlerin entropisinin asla azalmayacağını belirtir. Bunun sebebini izole sistemlerin termodinamik dengeden spontane olarak oluşmasıyla açıklar. Buna benzeri olarak daima çalışan makinelerin ikinci kanunu imkansızdır.
İkinci yasa ünlü bir sıcaklık ölçeğine müsaade verir. Bu ölçek özel ve bağımsız bir ısıbilgisi sistemin özelliklerini tanımlar. İkinci yasa farklı birçok formda açıklanabilir ancak birinci formulasyon 1824 yılında Fransız bilim adamı Sadı Carnot tarafından yazılmıştır. Ikinci yasanın birinci tabirleri sadece yatay düzlemde (yerçekimisiz alanda) doğrudur. Ikinci yasa, iç güç U’ya eşit olarak kapsamlı özelliklerin işlevi olarak da yazilabilir.
13. Genel Görelilik
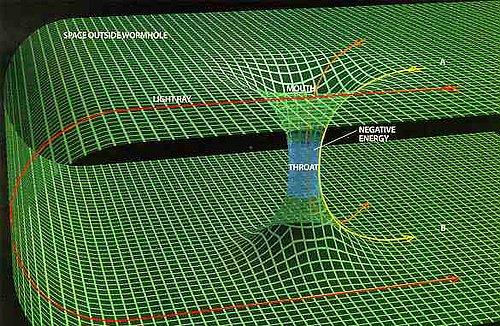
Genel görelilik ya da göreliliğin genel kuramı, 1916 yılında Albert Einstein tarafından yayımlanan kütleçekimin geometrik kuramıdır. Günümüzde modern fizikte kütle çekimi tanımladığı düşünülen kuramdır. Genel görelilik, özel görelilik ve Newton’ın üniversal kütleçekim yasasını genelleştirerek kütleçekimin uzay ve zaman ya da uzayzamanda tanımlanmasını sağlar.
Einstein’in teorisinin astrofiziğe kayda paha tesirleri vardır. Örneğin, büyük bir yıldızın ömrünün sonuna yaklaştığı bir vakitte içine çökerek karadelik oluşturduğuna işaret eder. Kimi astronomik cisimlerin yaydığı yoğun radyasyona karadeliklerin sebep olduğuna dair kâfi delil mevcuttur. Genel görelilik birebir vakitte, bugüne kadar fakat dolaylı olarak gözlenmiş olan, kütle çekim dalgalarının da varlığını öngörür.
Genel göreliliğin bugüne kadarki tüm önermeleri deney ve müşahede ile doğrulandı. Her ne kadar genel görelilik kütleçekimin tek izafî kuramı olmasa da, deneysel bilgi ile ahenk sağlayan en kolay teoridir. Buna karşın, teorinin hala cevaplayamadığı sorular varlığını sürdürmektedir. Bunlara örnek olarak pioneer uydusunun hareketi, galaksilerin dönüş eğrisi, genel görelilik ile kuantum mekaniği maddelerinin hangi halde bağdaştırılarak, tamamlanmış ve kendi içinde dengeli bir kuantum alan kuramı yaratılabileceğidir.
14. Schrödinger Denklemi

Schrödinger denklemi, bir kuantum sistemi hakkında bize her bilgiyi veren araç dalga fonksiyonu adında bir işlevdir. Dalga işlevinin uzaya ve vakte bağlı değişimini gösteren denklemi birinci bulan Avusturyalı fizikçi Erwin Schrödinger’dir. Bu yüzden denklem Schrödinger denklemi ismiyle anılır. 1900 yılında Max Planck’ın ortaya attığı “kuantum varsayımları”nın akabinde, 1924 de ortaya atılan de Broglie varsayımı ve 1927’de ortaya atılan Heisenberg belirsizlik ilkesi bilim dünyasında yeni ufukların doğmasına sebep olmuştur. Bu gelişmeler Max Planck’ın kuantum varsayımları ve Schrödinger’in dalga mekaniği ile birleştirilerek kuantum mekanik kuramını ortaya çıkarmıştır.
15. Bilgi Kuramı

Bilgi kuramı, Claude E. Shannon tarafından inançlı şekilde veri sıkıştırma, depolama ve iletme üzere sinyal sürece süreçlerinin kısıtlarını bulmak için geliştirilmiştir.
Bilginin değerli bir ölçütü, çoklukla depolama ve irtibat için gerekli olan modüllerin ortalama sayısı olan entropidir. Entropi, bir rastgele değişkenin bedelini varsayım ederken meçhullüğü nicelikselleştirir. Örneğin, bir yazı çeşide oyununun sonuç için sağladığı bilgi, bir zar atma oyununun sonuç için sağladığı bilgiden daha azdır. Yazı cinse oyununda eşit olasılıklı iki sonuç vardır, zar atma oyununda ise eşit olasılıklı altı sonuç. Bu nedenle yazı çeşide oyunu daha düşük entropiye sahiptir.
Bilgi kuramının temel uygulamalarına örnek olarak kayıpsız bilgi sıkıştırma (ZIP dosyaları), kayıplı bilgi sıkıştırma (MP3 dosyaları) yahut kanal kodlama (DSL bağlantıları) gösterilebilir. Bilgi kuramının alanı matematik, istatistik, bilgisayar bilimi, fizik, nörobiyoloji ve elektrik mühendisliği ile kesişir. Voyager derin uzay vazifeleri, kompakt diskin geliştirilmesi, cep telefonlarının yapılabilirliği, internetin geliştirilmesi, dilbilim araştırmaları üzere pek çok mevzuda muvaffakiyetin üzerinde büyük tesiri olmuştur. Bilgi kuramının kıymetli alt kısımları; kaynak kodlaması, kanal kodlaması, algoritmik karmaşıklık kuramı, algoritmik bilgi kuramı üzere alanlardır.
16. Kaos Teorisi

Kaos kuramı, kaos teorisi veya kargaşa kuramı; yapısal olarak bir fizik teorisi ya da matematiksel bir tümevarım değil, fizikî gerçeklik modüllerinin bir bütün olarak eğilimini açıklamaya yarayan bir sistemdir.
Bir sigara dumanının havada yaptığı haller büsbütün sistemsiz ve bağımsız tesadüflerin eseri olarak görülebilir. Lakin bir teorik fizikçi dumanın bu dinamiğinin aslında ortamdaki birçok parametre ve etken ile belirlendiği görüşündedir. Bu girdiler o kadar çoktur ve o kadar değişkendir ki incelemek ve net bir kanıya varmak imkânsızdır. Parametrelerin bu kadar değişken olması aslında o parametrelerin de bir çıktı olmasından kaynaklanır. Dumanın hareketine neden olan hafif bir hava akımı aslında odanın öteki yerindeki bir sıcaklık değişikliği ve basınç farkının neden olduğu bir harekettir. Ayrıyeten dumanın dinamiğini etkileyen girdiler birbirlerine bağlı olabilirler ki bu durumu tam manasıyla içinden çıkılmaz hale sokar.
Teoriye temel oluşturan matematiksel ve temel bilimsel bulgular 18.yüzyıla, hatta birtakım gözlemler antik çağlara kadar geri gitmektedir. Yunan ve Çin mitolojilerinde yaradılış efsanelerinde başlangıçta bir kaosun olması tesadüf değildir. Özellikle Çin mitolojisindeki kaosun, bugün bilimsel lisanda tanımladığımız olgularla hayret verici bir benzerliği olduğu görülür. Batı’da da daha sonraki devirlerde bilim adamları tarafından karmaşık olgulara dair müşahedeler yapılmıştır. Poincare, Weierstrass, von Koch, Cantor, Peano, Hausdorff, Besikoviç gibi çok üst seviye matematikçiler tarafından bu teorinin temel kavramları bulunmuştur.
17. Black-Scholes Eşitliği

Black Scholes Eşitliği, 1973 yılında Fischer Black ve Myron Scholes tarafından yazılan makalede birinci sefer bahsedilen opsiyon fiyatlama tekniğidir. O vakte kadar yapılan en yeterli modellemedir ve hala kullanılmaktadır.
Bu model rassal hareketler izleyen sıvı moleküllerini ortaya koyan Brownian Motion’ın pay fiyatlarına ve finansal hareketlere uyarlanması sonucu ortaya çıkmıştır. Robert C. Merton’un modelde çözülemeyen bir kısmı çözmesinden sonra, bu model Black-Scholes-Merton Modeli olarak anılmaya başlamıştır.


